Refinement and Canonization of the Herophilean Pulse Rhythm Theory – Galen (129-ca. 200/216 AD)
The Greek Κλαύδιος Γαληνός – Klaúdios Galênós, Anglicized as Galen, was born in Pergamon in the first half of the 2nd century AD. He died in the first decades of the following century. He studied and traveled widely in the Roman Empire before settling in Rome, where he served prominent members of the Roman society and was finally given a position in the imperial court as personal physician to several emperors, among others Marcus Aurelius and his son Commodus.
As his immediate Pneumatic predecessors, Galen acknowledges Herophilus’ groundbreaking achievement concerning the observation of pulse rhythm. He is also willing to accept his basic definition of rhythm as “ratio of the time of the motions.”
Let it the be established, for practical purposes, that rhythm consists in the ratio of the time of the motions [τοῦ χρόνου τῶν χινήσεων τὸν ρυθμὸν συνὶστασθαι – toû khrόnou tôn khinêseôn tòn rhuthmòn sunístasthai], since we will at some point make a separate inquiry about Herophilus’ view. (Galen, De dign. puls., 3.3, 8.912-913, trans. Heinrich von Staden)
He develops a similar classification of pulse rhythms according to the degree of deviation from “natural rhythm.” According to him, the pulse rhythm can be either “natural,” when the patient is sound, or “contrary to nature,” when he or she is ill. In this case, it can be either “pararhythmic” (with the smallest deviation), “heterorhythmic” (with a greater deviation), or “ecrhythmic” (with the greatest deviation). It is therefore a very precise and irreplaceable diagnostic technique.
In comparing the time of dilation [of the pulse] to the time of the contraction, as Herophilus thought one should, it can be recognized that the ill person has [a pulse] contrary to nature [παρὰ φύσιν – parà phúsin], and in addition that it is greatly or negligibly contrary to nature [παρὰ φύσιν – parà phúsin]. For, great deviations from the natural rhythms [τῶν κατὰ φύσιν ῥυθμῶν – tôn katà phúsin rhuthmôn] into that which is contrary to nature [τὸ παρὰ φύσιν – tὸ parà phúsin] signify great harm, whereas lesser deviations signigy smaller harm. For the para-rhythmic pulses [οἱ παράῥυθμοι σφυγμοί – hoi parárhuthmoi sphugmoí] display the smallest deviation, heterorhythmic pulses [οἱ ἑτεροῥυθμοι – hoi heterorhuthmoi] a greater deviation, and ecrhythmic pulses [οἱ ἔκῥυθμοι – hoi ekrhuthmoi] the greatest. (Galen, Synopsis librorum suorum de pulsibus, 14, 9.470, trans. van Staden, my mod.)
Galen also notices in passing that it would be possible to apply Herophilus’ pulse rhythm theory to respiration—showing incidentally that this association was not yet a regular feature in 2nd century AD medicine. Contrary to what appears in von Staden’s translation, who tries to be as clear as possible and expands Galen’s somehow concise expression, he does not use the term “respiratory rhythm” but the idea is clearly already there.
It is clear that the same speculation as was recorded by Herophilus concerning rhythms in the pulse will await this part [sc. the parts used in respiration, since the respiratory “rhythms” of inhalation and exhalation are not unlike the diastolic and systolic rhythms of the pulse]. (Galen, De difficultate respirationis, 1.21, 7.812, trans. and com. Heinrich von Staden)
However, his relationship to Herophilus’ pulse lore is not one of slavish imitation. He disagrees with him principally on three accounts although with varying intensity.
Firstly, as Pliny, he remarks that Herophilus’ concept of rhythm has become difficult to understand because it necessitates the reader be correctly acquainted, thanks to a proper education, with rhythm in musical and poetic context. He also criticizes the systematic approach that is used by Herophilean physicians and accuses them to be so enchanted with Herophilus’ rhythmic system that they cease to bother with predicting the course of the diseases they have to deal with and forget the very purpose the system was developed for. It seems, however, that both reproaches are addressed to his contemporary competitors, whose lack of culture and dogmatism he contemptuously mocks, more than to Herophilus whom he admires and considers as having cleverly taken “what was useful from the musicians into medicine.”
For this reason anyway whatever about rhythms of music they ought to have learned while they were still children in the schools they in no way bring to treatises of medicine, suffering the ill-effect of their late learning, nor can they keep silent, even if [the subject] belongs to another art. No one of them wrote how one ought to make meaning from rhythm. But Herophilus at least, going a route opposite to them, leaves out what someone worthily educated of the art should have learned from musicians, and speaks to them as if they understand, since he takes what is useful from them into medicine. But they, whenever they detail this amazing system [τεχνολογίαν – tekhnologίan]—as they call it— about rhythms, they no longer care to show how one might sufficiently make prognoses or interpret through these things. (Galen, De dignoscendis pulsibus 2.3, 8.871-872, trans. Berrey)
Secondly, Galen feels necessary to enlarge Herophilus’s pulse definition (I am using for this section and the next Berrey, 2011, p. 215 sq.). Whereas the latter used four main criteria to differentiate between pulses (size, speed, strength, concerning one dilation beat, and rhythm concerning the relation between dilation and contraction), he sets up a classification based on eight generic differentiae (De pulsuum differentiis, 1.3, 8.501 and De pulsibus ad tirones, 2-7, 8.455-59). He first accepts size, speed, and strength of the artery’s movement, and rhythm, which he defines, similarly to Herophilus, as the ratio of the time of dilation to the time of contraction. But he adds to this list two more groups of differentiae. One concerns the state of the artery: the hardness of its tunic; and the fullness of its body. The other strikingly complements the rhythmic measure by enlarging the observation over a longer series of beats: the frequency of the arterial beat and pause, which was also used by Herophilus without being considered a full differentia; and its regularity, which instead is an entirely novel feature ant tries to figure out if the beat, observed over a longer time, is regular, oscillating or totally irregular.
Since the artery has three dimensions, just as any other body—length and breadth and depth—it is entirely necessary that in each of the dimensions there be some quantity of dilation and contraction. It is further necessary that it have tension, either weak and faint, or readily and strongly active; and that the tunic itself of the artery either be soft or hard, but that the internal width either be empty somehow or full; and that in all these things there occurs at some time a regularity and at some time an irregularity; and that there be some ratio of the time-unit of the dilation to that of the contraction; and that beyond these no other differentia can occur in one pulse. (Galen, De pulsuum differentiis, 1.3, 8.501, trans. Marquis Berrey)
Actually the only point on which Galen really disagrees with Herophilus concerns the measure of rhythm. He contends that Herophilus’ view is somehow confusing. The latter does not clearly say whether he thinks of it only as “a ratio of the time of dilation to the time of contraction” or as a more complex measure that would encompass also “the time of rest which follows upon each of the two motions.”
In all these things many insoluble difficulties necessarily occur in the [medical] factions in differentiation of rhythms, and I think it is for this reason that physicians after Herophilus did not even attempt to write anything on prognosis based on rhythms. And while Herophilus himself in many places mentions rhythms with a view to prognoses, it is very difficult to discover just what he means by “rhythm” [τὸν ῥυθμòν– tòn rhuthmòn]: is it the ratio [τὸν λόγον – tòn lógon] of the time of dilation to the time of contraction only, or does he also attribute to “rhythm” the time of [rest] [ἠρεμίας – êremías] which follows unpon each of the two motions? This is where there is no agreement, not even among those who are named “Herophileans” after him, concerning just what Herophilus really thought about rhythms. For his words do not indicate one of the two alternatives clearly, nor is the nature of these things capable of providing confirmation. (Galen, De dign. puls., 3.3, 8.911-913, trans. Heinrich von Staden, my mod.)
Whereas his predecessor distinguished only two kinds of arterial motion, Galen emphasizes the need to pay attention to the pauses or inactive intervals in the pulse cycle. He identifies four times in each cycle of arterial pulsation: dilation / pause / contraction / pause. The rest following dilation he calls ἡ ἐκτὸς ἠρεμία – hê ektòs êremía – external rest, because it happens at the peak of the artery’s outward expansion toward the touch of the physician. The other following contraction he calls ἡ ἐντὸς ἠρεμία – hê entòs êremía – internal rest, because it happens at the nadir of the artery’s inward contraction away from the touch of the physician (Berrey, 2011, p. 52, n. 7).
He also notices that the first part of the dilation and the final part of the contraction are almost imperceptible (De discognendis pulsibus, 3.3, 8.909-910). The only part that can be measured with accuracy is the final part of the dilation (De discognendis pulsibus, 3.3, 8.903). This leads, Galen notices, to the unsatisfactory conclusion that, according to Herophilean standard, the rhythm could be accurately measured only in vehement pulses, without incidentally being determined precisely enough since the perceptible part of dilation would be taken in relation to all the remaining parts, namely contraction and the two rests (Berrey, 2011, p. 216).
His own solution to the problem is exposed at the very end of Book 3 of On Distinguishing Pulses. He proposes to measure each dilation and contraction relatively, from whatever part of it can be perceived by touch. Should the physician want to rate, for instance, the pulse speed, he may content himself with rating the dilation fast, moderate, or slow, and doing likewise for the contraction. The combination of both arterial motions should then be located among those on a chart reproduced here below that is applicable for any pulse except the dullest, whose parts are not perceptible. The physician thus avoids the problem initially identified: the impossibility to measure the entirety of the arterial motions. In Galen’s method there is no need to measure the full cycle, since any perceptible part is taken to stand for the whole (Berrey, 2011, p. 217).
What meaning each differentia has we will make clear in On Prognosis. But now we will first subscribe the chart, since it will be readily clear to those trained in the first book of On Differentiae of Pulses. Following we will say in what way again many differentiae exist differing from each other in quantity, even if they are of the same kind.
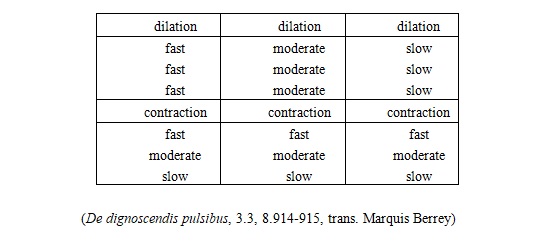
This empiricist stress on perception results in a critique of Herophilus’ descriptions of pulse rhythm that are deemed too vague even if the concept of proportion of time-lengths can be useful.
It became clear, on the basis of the things he [Herophilus] did teach, that he is confused and does not clearly articulate the distinction between contraction and rest [pause]. For, if he actually thinks that a contraction which is extended for as long as ten primary time-units can arise in old people, he very clearly is not perceptive about what a contraction really is. You see, sometimes it is of shorter duration than the dilation, sometimes of equal duration, and at other times, as he writes, of longer duration—but not, as he thinks, five times as long; rather, only a little more. (Galen, De praesagitione ex pulsibus., 2.3, 9.278-279, trans. Heinrich von Staden)
It also results in the rejection, as too simplistic and inadequate, of Herophilus’ use both of the Aristoxenian quasi-mathematical concept of πρωτος χρόνος – prôtos khrónos—“we had no need of primary time-unit”—and of the four binary metric feet as main types of arrangement of the prôtoi khrónoi.
Instead Galen elaborates a very refined classification of rhythmic cycles which presupposes their very variability without losing its precision. “Many differentiae”—unfortunately he does not list them but we may also think of size and strength—are to “differ from each other in quantity, even if they are of the same kind.” Galen takes again the example of the speed of the successive motions (dilation and contraction), which can be rated as greater or smaller “by a small degree” or “by a lot.” Therefore, whereas Herophilus, using elementary arithmetics, measured very simple ratios of time-lengths (1/1, 2/1, 2/2, 1/2), Galen introduces the idea, presupposing a more advanced mathematics, that rhythm should be defined as ratio of varying quantitative measures.
Since the first differentiae written in the chart have a fast motion, it indicates that the motion in dilation is spurred on to the greatest degree, and the motion in contraction is greater by a small degree than the moderate and medium motion, or on the other hand that the motion in dilation is greater by a little, and that the motion in contraction is much greater or both are greater by a little or both by a lot, or the one by a little, the other by a lot, or less by a little or by a lot, or however else. The variety is obvious. It is not possible to say either that this seems not to happen, or that it has no meaning. For indeed it happens and very much has meaning. For us it sufficed to make prognoses from this distinction, since we had no need of primary time-units, both whole in their parts and enlarged [τῶν πρώτων χρόνων ὁλοϰλήρων τε ϰαὶ παρηυξημένων – tôn prôtôn khrónôn holoklêrôn te kaì parêuxêménôn]. That such a distinction needs no entire motion but can become clear to anyone through a chance part of it, except if it should be unequal (for then the part is not equal to the whole). Moreover not even in very dull pulses is it possible to employ this method. For it is not possible in the case of these pulses to recognize the first beginning of the contraction, not any part of it is worthy of record. (De dignoscendis pulsibus, 3.3, 8.915-916, trans. Marquis Berrey)
It has often been claimed that some of these complex rhythms were given by Galen evocative names, sometimes borrowed from the Pneumatics, because they were easy to remember: “goat-like,” “ant-like,” “worm-like,” “rat’s tail-like,” etc. Some 19th century commentators viewed these names as “charming metaphors” that “naturally” could not be used any longer by “modern science.”
But one may also notice that in Galen’s new account rhythm becomes less static and more dynamic, less mechanical and more “life-like,” and that may explain why he chose metaphors referring the most typical complex pulses to animal movements implicating both varying ratios between dilation and contraction, frequency, and more or less regular succession of beats. The pulsus caprizans, for instance, was named after the goat because it had a double impulse, a small one followed quickly by a larger one, before coming down again—like the leap of a goat. The fatal pulsus vermicans and formicans resembled the frenetic movement of a worm or that of an ant. The pulse myuri was like the movement of a rat tail since it gradually became smaller, and in like manner recovered its magnitude gradually, and so on alternatively.
Furthermore, since it presupposes that the ratio determining the rhythm concerns varying quantitative measures, it cannot be reduced anymore to rational numbers or simple fractions, and must admit irrational solutions. Considering Galen’s care in describing the variation of the difference between the various quantities of the dilation and the contraction—“ that the motion in contraction is much greater or both are greater by a little or both by a lot, or the one by a little, the other by a lot, or less by a little or by a lot, or however else” —one even wonders if the proto-calculus developed by Archimedes might not be here at work beneath the surface. This would need to be investigated more thoroughly than I can afford here. Suffice it to note, for the time being, that these phenomenologically animal-like and mathematically irrational rhythms could be easily represented with graphs. Joseph Struthius who wrote an Ars sphygmica in 1540 seems to have been the first to attempt at a graphic representation of the form of the pulse derived from his study of the movement of a leaf laid on a superficial artery (Fleming, A Short History of Cardiology, 1997, p. 20). In his Medicine dissertation (Berlin, 1866 quoted in Deichgräber, 1981, p. 294, n. 1), Otto Schadewald has proposed a very suggestive graphic model for the pulsus caprizans showing a repeated sequence of double impulses in the dilation followed by a swift contraction.
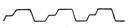
It is most unlikely that Galen ever graphed or even imagined such kind of oscillating curves which began to be commonly available only with Carl Ludwig’s Kymograph (1847) and Etienne Marey’s Sphygmograph (1860). But, just as Herophilus who introduced frequency as a significant aspect of pulse rhythm without yet making it part of its definition, Galen certainly provided, with his improved quantification technique, new elements prefiguring the future mutation of the concept of pulse rhythm from a succession of time-lengths organized according to metric proportions, in the Ancient poetic and musical sense, to a more modern metric model based on continuous repetitive variations.

